Os fractais são estruturas geométricas complexas e autossimilares encontradas em diversos ramos da matemática e na natureza. O termo “fractal” foi cunhado pelo matemático Benoît Mandelbrot, que explorou a origem e o funcionamento dessas formas em sua obra “Fractal Geometry of Nature”.
Em sua essência, fractais exibem uma propriedade notável chamada autossimilaridade, o que significa que sua estrutura é repetida em diferentes escalas. Independentemente do nível de ampliação, a mesma forma básica persiste. Isso cria padrões intrincados e belos que se assemelham a formas naturais encontradas em flocos de neve, conchas, nuvens, montanhas e até mesmo sistemas biológicos.
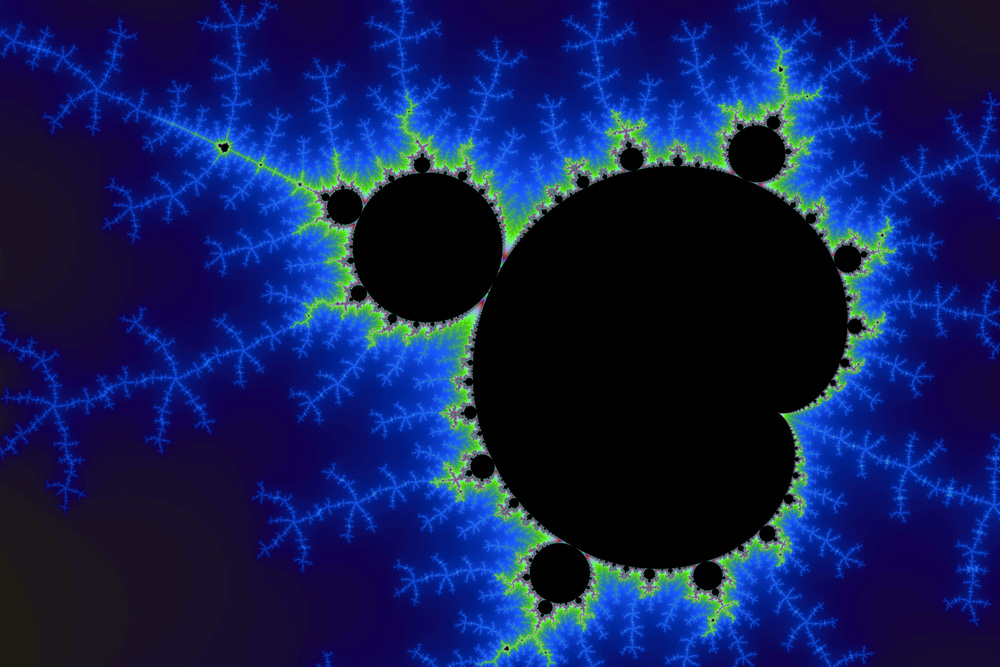
Um exemplo clássico de um conjunto fractal é o conjunto de Mandelbrot. Gerado por meio de iterações simples, esse conjunto revela estruturas complexas que se repetem infinitamente. A beleza do conjunto de Mandelbrot reside na sua capacidade de criar formas complicadas a partir de regras matemáticas aparentemente simples.
A diversidade dos Fractais
Fractais não se limitam à matemática abstrata. Eles têm aplicações práticas em diversas áreas, como modelagem de terrenos, compressão de imagens, antenas de microfita e até mesmo na compreensão de padrões na atividade cerebral. Sua presença na natureza destaca a conexão complexa entre a matemática e o mundo que nos rodeia.
Além disso, os fractais encontraram um bom lugar na arte. Alguns artistas exploram essas formas para criar obras visuais impressionantes, capazes de capturar a imaginação do observador. A combinação de precisão matemática e expressão artística ressalta a interseção entre ciência e criatividade.
Um exemplo disso é o trabalho do artista visual Alex Gray, que por meio de um estilo artístico psicodélico e rico em detalhes, utiliza padrões fractais para compor as suas obras, criando composições visuais extremamente vibrantes.
Em sua essência, os fractais transcendem a mera geometria; eles se tornam portais fascinantes para desvendar a complexidade intrínseca do universo. Vão além da matemática pura, influenciando a resolução prática de problemas e inspirando expressões artísticas. Ao revelar a beleza da autossimilaridade, essas estruturas geométricas surgem como testemunhas da diversidade que permeia o nosso mundo.